System Identification
System identification deals with building a mathematical model of the input-output behavior of a dynamical system from measurements of its input and output signals. The Automatic Control group has contributed to this highly active field over many years, both in terms of theory, algorithms, applications, and software.
The current activities concern
Nonlinear systems
Estimation of nonlinear models is a challenging problem and we are working on topics like how to design efficient estimation methods, how to test for the presence of nonlinearities, how to handle data from closed-loop experiments, how linear models can be used to approximate nonlinear systems, and how to provide a practical "user's guide" to all the choices available. Some application examples are aircraft, industrial robots, and power-efficient electronic devices.
Dimension reduction
Dimension reduction concerns finding appropriate reformulations of system descriptions in order to obtain lower-dimensional nonlinear modeling problems and we are investigating several approaches. A second type of dimension reduction is found in applications where a large number of signals are measured, such as fMRI (magnetic resonance imaging) experiments in medical applications. Here, the dimension of the measurement space has to be reduced.
Regularization and links with machine learning
Finite impulse response models and autoregressive models with extra inputs are very common and simple models of dynamical systems and can be written as linear regression models. It is advantageous to allow some regularization when solving the corresponding linear least squares estimation problems since this enables a much better variance/bias trade-off in the solution. This has close links with Bayesian modeling, so-called Gaussian process regression in machine learning and reproducing kernel Hilbert spaces techniques in statistics. A major challenge is to find the best ways to parameterize and tune the regularization matrix.
Parameterization issues and convex formulations
A typical approach to identification is to minimize a criterion of fit with respect to model parameters. These criteria are generally non-convex functions, and it is an important open problem to find ways to parameterize and convexify the functions to be minimized. A well-tuned regularization is one way to achieve this, even though the tuning itself may need to be convexified. Other ways are to consider algebraic techniques to analyze the parameterization and exploit subspace methods for initializations.
Examples

For large vehicles, such as container ships, mounted inertial sensors will move relative to each other because of flexibility in the structure. This results in interesting estimation problems since the sensor outputs will depend both on time and position.
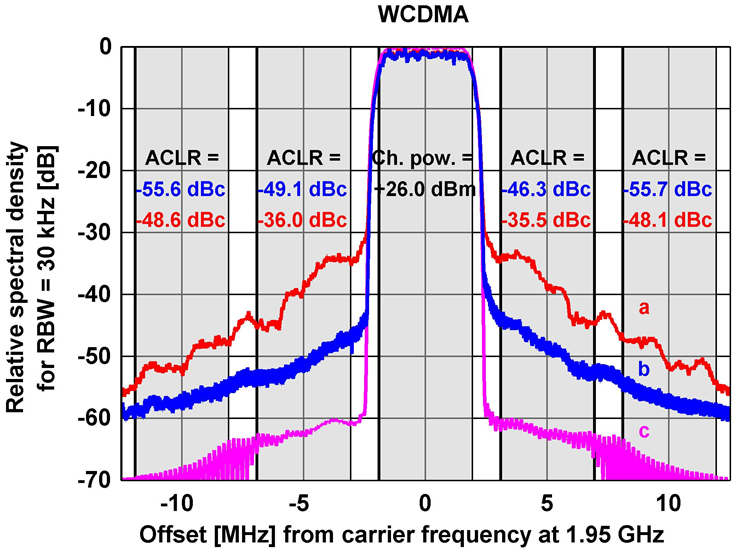
Nonlinear power amplifiers can be made more power efficient than linear power amplifiers, but have to be linearized with a model-based predistorter. Spectrum c (pink) is the input to and spectrum a (red) is the output from the power amplifier, without any correction. Line b (blue) describes the output spectrum when a predistorter is applied. The nonlinearities are clearly reduced.
Informationsansvarig: Lennart Ljung
Senast uppdaterad: 2022-06-23
 LiU Homepage
LiU Homepage
